와 벌써 6강!
1. 버텍스 칼라 응용2
2. 벡터 이론
1. 버텍스 칼라 응용2
응용하는 방식은 저번이랑 비슷합니다
1 - smoothness
2 - normal
1 - smoothness

저번에 타일 깔던 것과 비슷하게
smoothness를 먹이고 싶은 곳을 r/g/b중 골라서 칠한 다음, 그 값을 smoothness에 꽂아주면 됩니다
그럼 칠한 부분은 1이 먹을 것이고, 안칠한 부분은 0이 먹겠죠

이런 식으로요
근데 좀 쎄서 줄이고싶다 하면 0 ~ 1 사이의 값을 곱해주면 되겠죠
뭐 예를 들면 0.3이라던가, 0.8이라던가 등등...
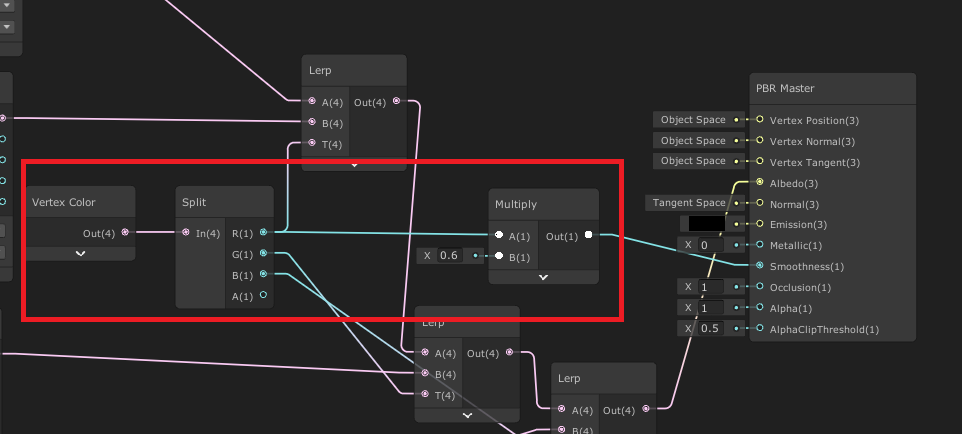
이렇게 마스터노드에 꽂기 전에 0.6을 곱하면

많이 약해진 걸 볼 수 있습니다
2 - normal
여기서도 버텍스칼라 채널 하나 뽑아와서 쓰는건 맞는데
smoothness는 그냥 0~1 사이의 값 하나 넣어주면 끝이라 버텍스칼라 그대로 넣어도 상관이 없었어요
하지만, normal은 어떻게보면 텍스쳐를 적용시키는 작업이기 때문에 노말은 약간 추가 작업이 필요합니다
여기서 저번에 썼던 Lerp를 사용합니다

Lerp 복습을 하자면, A와 B를 합쳐주는데 T가 0에 가까워질 수록 A에 가까운 값을 출력하고, 1에 가까워질 수록 B에 가까운 값을 출력하는 함수였죠
일단 버텍스칼라중 자신이 칠했던 채널을 빼와서 T에 꽂아줍니다 그럼 칠한 부분(노말을 입히려고 하는 부분)은 값이 1이 될것이고, 그렇지 않은 부분은 값이 0이겠죠
그럼 이제 T값이 1에 가까워질 수록 B에 가까운 출력이 나온다고 했으니까 B에 노말텍스쳐를 꽂아줍니다
그리고 A에는 노말이 안들어간(기본값)인 (0,0,1)을 넣어줍니다(Lerp 특성상 w도 추가되었지만 쓰레기값이니 무시하면 됩니다)
그리고 저 Lerp에서 나온 값을 마스터노드의 Normal에 꽂아주면

이렇게 우리가 칠했던 부분만 normal이 먹는 결과물을 볼 수 있습니다
2. 벡터 이론
1 - 벡터의 뜻
2 - 단위벡터
3 - 벡터 연산
1 - 벡터의 뜻
방향을 나타냅니다

수많은 화살표가 있지만, 뻗어나가는 방향은 모두 똑같이 오른쪽 위 인걸 볼 수 있죠
다 같은 벡터라고 볼 수 있습니다
그리고 "어느 방향으로 나갈 것인지"가 중요한 것이기 때문에 시작점은 그냥 0으로 고정해놓고,
끝 점의 위치만 부릅니다

이런 벡터가 있다 치면 (1,1)로 쓰지, (0,0)->(1,1) 뭐 이런식으로 쓰지는 않는다는 거죠
2 - 단위 벡터
벡터의 크기가 1인 벡터를 말합니다
계산할 때 기준이 되는 값? 그런 느낌이라고 보면 될 것 같네요
크기 구하는 공식은

이거고, 이 값이 1이 나오는 벡터가 단위 벡터라는 것이죠
그리고 어떠한 벡터의 크기를 1로 만드는 걸 "벡터의 정규화"(normalize)라고 부릅니다
다른 벡터와 연산할 때의 기준이기 때문에 방향벡터 연산할 일이 있으면 단위 벡터로 만들어야 정확한 결과가 나옵니다
3 - 벡터 연산
뭐 특별할 거 없어요
(스터디 간접참여)유니티 SRP 셰이더 그래프 - 2
히히... 이것만 쓰고 언리얼하러가야지...... 이번시간엔 뭔가 여러가지 했네요 1. 각 Vector들 끼리의 연산법 2. Vector 찢기 / 다시 붙이기 3. Vertex에 들어있는 정보들 4. 예시용 필터 만들기 1. 각 Vector들..
gimchicchige-mukgoshipda-1223.tistory.com

저 위에서 설명했던 요거
이걸 그냥 좌표계에 올려놓은거 뿐이거든요
그래도 일단 한번 그림으로 봐봅시다
(2,1)+(1,2) 를 한번 해보죠

이 두개를 더한다는 겁니다
더하면 어떻게 되나

이렇게 되서 결과 값으로는 (3,3)이 나옵니다
벡터 모양은

저 주황색 선같은 방향이 나오는 것이죠
'그래픽(기타)' 카테고리의 다른 글
| 유니티 SRP 셰이더 그래프 - 8 (0) | 2020.01.23 |
|---|---|
| 유니티 SRP 셰이더 그래프 - 7 (0) | 2020.01.19 |
| 유니티 SRP 셰이더 그래프 - 5 (0) | 2020.01.10 |
| 유니티 SRP 셰이더 그래프 - 4 (0) | 2020.01.09 |
| (SRP)쉐이더 서브그래프 제작 - SimpleRaderMask (0) | 2020.01.06 |